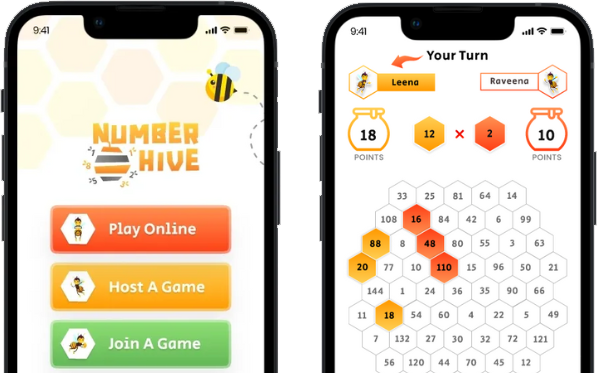
Number Hive Printable Game Boards
Expand your Number Hive game play into addition, fractions, algebra and much more with our printable game boards. Perfect for extending learning, or unlocking the power and equity of blended learning.
🌶️ MILD Game Board Packs – Addition & Subtraction

Addition: Dice (1-6)
Build additive reasoning and subitizing skills for learners starting out with addition.
Perfect for ages 4-7
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Integers 1-12
Perfect for mastering addition. Encourage confident learners, build additive fluency, and strengthen the relationship between the inverse operations; addition and subtraction.
Perfect for ages 6-9
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Subtraction: Integers
Build fluency and proficiency with basic subtraction. Our first subtraction version ever also helps build an understanding of inverse relationships.
Perfect for ages 6-10
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Time
Helping students work with adding amounts of time but also in converting the different units of time.
Perfect for ages 6-11
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Integers -6 to +6
Build fluency and understanding of the notoriously difficult concept of adding integers when negative numbers are involved.
Perfect for ages 7-13
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Understanding Fractions STEP 0
Build conceptual understanding of fractions. This is STEP 0 of 3. Students will match fractions with their visual representation.
Perfect for ages 6-9
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
🌶️ MILD Game Board Packs – Multiplication (& Division)

Understanding Fractions STEP 1
Build conceptual understanding of fractions. This is STEP 1 of 3. Students will construct fractions using the numerator and the denominator with no simplification required and fractions <1.
Perfect for ages 6-10
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!
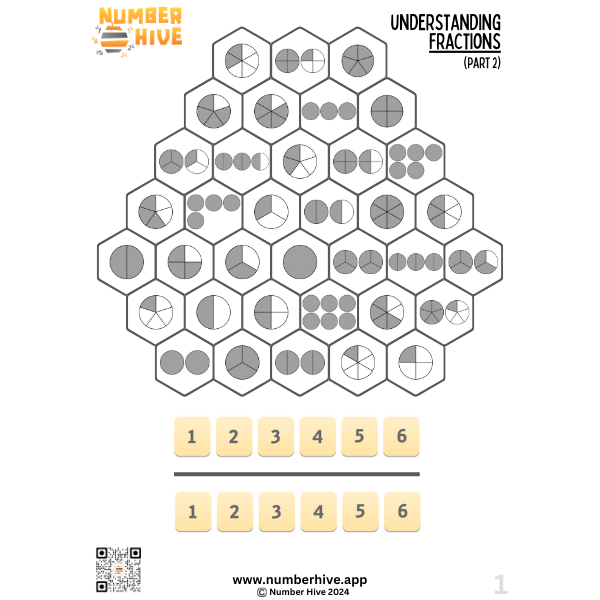
Understanding Fractions STEP 2
Build conceptual understanding of fractions. This is STEP 2 of 3. Students will construct fractions using the numerator and the denominator with no simplification required and fractions >1.
Perfect for ages 6-11
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Understanding Fractions STEP 3
Build conceptual understanding of fractions. This is STEP 3 of 3. Students will construct fractions using the numerator and the denominator with simplification required and fractions >1.
Perfect for ages 6-12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!
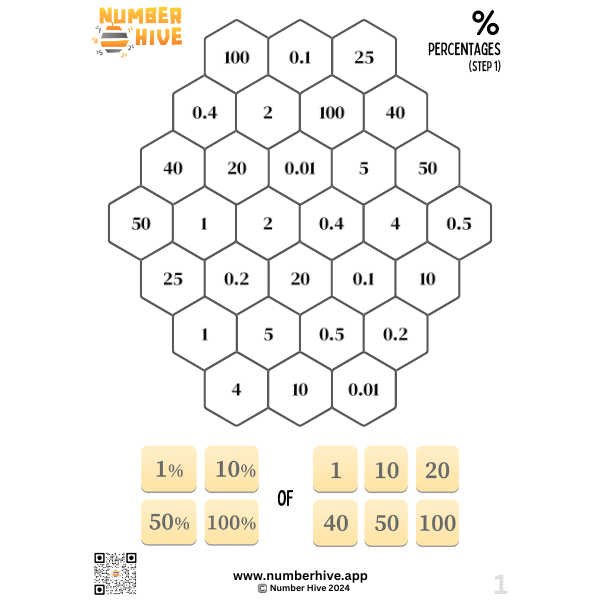
Calculating Percentages STEP 1
Build fluency in finding percentages of amounts. This is STEP 1 of 3. Students will find 1%, 10%, 50% and 100% of basic numbers.
Perfect for ages 9-13
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
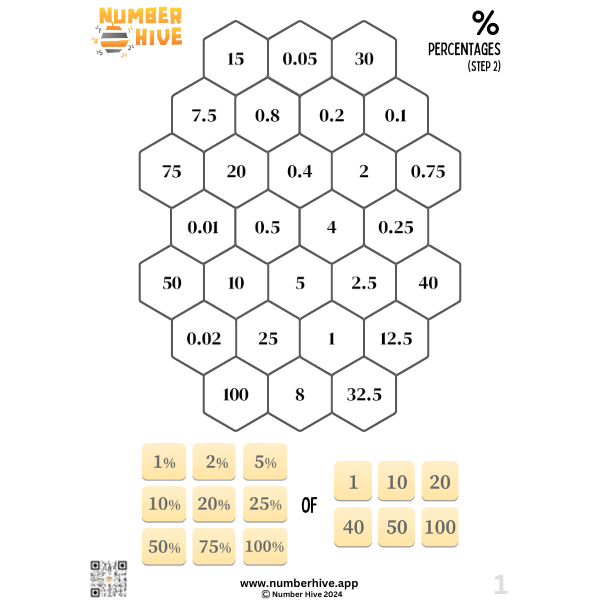
Calculating Percentages STEP 2
Build fluency in finding percentages of amounts. This is STEP 2 of 3. Students will find 9 different percentages of basic numbers.
Perfect for ages 9-14
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
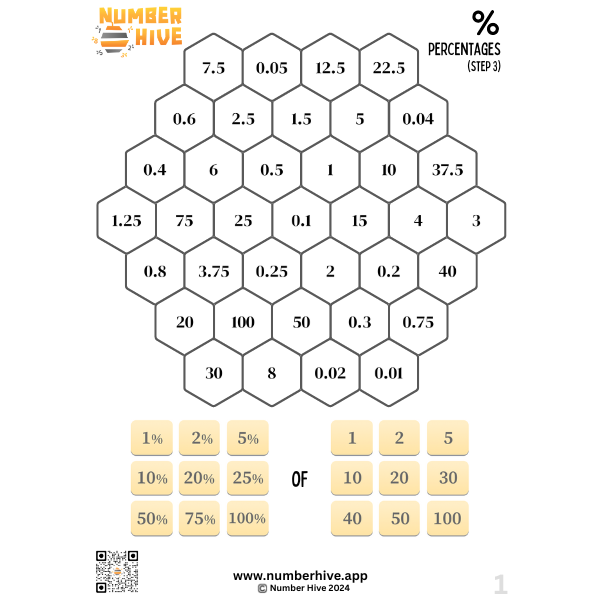
Calculating Percentages STEP 3
Build fluency in finding percentages of amounts. This is STEP 3 of 3. Students will find 9 different percentages of 9 different numbers.
Perfect for ages 9-14
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)

Multiplication: 1, 2, 3, 4, 5, 10
Master the earlier multiplication facts, deepen understanding, and sharpen mathematical thinking with the simple factors game board.
Perfect for ages 7-10
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: 1,2,3,4,5,10 & 1-12
Scaffold learning with this progression pack bridging the gap to mastery of 1-12 multiplication factors.
Perfect for ages: 7-10
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: 1-10
Build confidence and competence for learners focusing on the multiplication facts in the 1-10 range. Great for encouraging students without risking cognitive overload.
Perfect for ages 7-10
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: 1-12 (Times Tables)
The game you know and love is now printable, perfect for use as a stand alone classroom resource, or as the ultimate blended learning multiplication package.
Perfect for ages 8-13
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: Integers -6 to +6
Expand mathematical horizons with negative & positive integers. Build fluency in this extremely important foundation.
Perfect for ages 10-14
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: The Maze!!!
Brilliant for a ‘daily maze’ class challenge, or as homework (students explain the journey they took to get from the maze start to maze finish).
Perfect for all ages
Choices include:
- Small Group pack: 5 game boards
- Class pack: 40 game boards (40 Students)
Click here to watch a game!
🌶️🌶️ MEDIUM Game Board Packs – Addition

Addition: Fractions STEP 1
Build procedural fluency when adding fractions. This is STEP 1 of 5. Students will add fractions with common denominators and the sums unsimplified.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 7 – 11
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Fractions STEP 2
Build procedural fluency when adding fractions. This is STEP 2 of 5. Students will add fractions with common denominators and the sums simplified.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 7 – 12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Fractions STEP 3
Build procedural fluency when adding fractions. This is STEP 3 of 5. Students will add unit fractions with different denominators with the sums simplified.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 7 – 12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Fractions STEP 4
Build procedural fluency when adding fractions. This is STEP 4 of 5. Students will add fractions with different denominators with the sums simplified & left as improper fractions where >1.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 7 – 12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Addition: Fractions STEP 5
Build procedural fluency when adding fractions. This is STEP 5 of 5. Students will add fractions with different denominators with the sums simplified & left as mixed numbers where >1.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 7 – 12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!
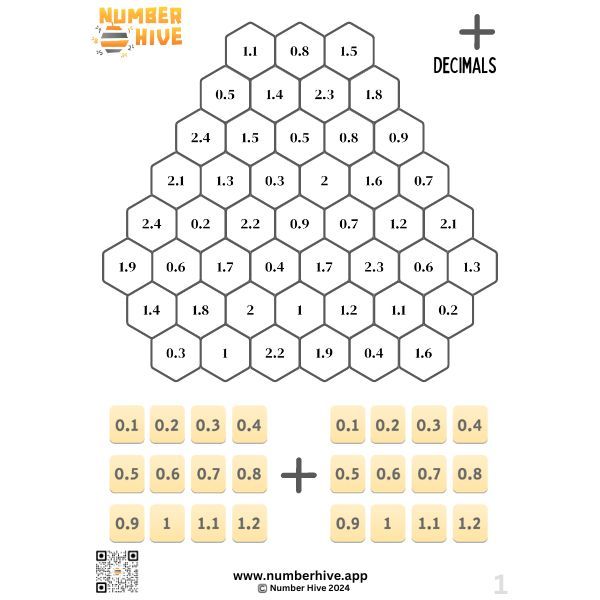
Addition: Decimals
Build procedural fluency when adding decimals. Students will add decimals which helps with understanding place value.
Information about this game board package:
-
Packs of 5 or 20 different game boards (PDFs)
-
Ideal for Ages: 8 – 12
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!
🌶️🌶️ Medium Game Board Packs – Multiplication (& division)

Multiplication: Decimals
Build fluency and proficiency with decimal multiplication and develop a deep understanding of decimal place value, and arithmetic.
Perfect for ages 11-14
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: Fractions
Explore multiplication of fractions, fraction equivalence, simplification and the relationship between fractions and whole numbers.
Perfect for ages 11-14
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!
🌶️🌶️🌶️ Spicy Game Board Packs – All operations

Multiplication: Algebra
Build fluency with algebraic operations. Foster a deep understanding of this foundational skill for any students studying higher levels of algebra down the track.
Perfect for ages 12-16+
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: Exponents/Powers/Indices
Working with exponents in the game helps develop a deeper understanding of algebraic relationships where powers are involved.
Perfect for ages 12-16+
Choices include:
- Small Group pack: 5 game boards
- Class pack: 20 game boards (40 Students)
Click here to watch a game!

Multiplication: Radicals, surds, square roots
Students can gain familiarity with radicals. Some regions call them surds, others square roots. Either way, these game boards will help students gain a deep understanding of operating and simplifying.
Perfect for ages 12-16
Choices include:
- Group pack: 5 game boards
- Class pack: 20 game boards
Click here to watch a game!
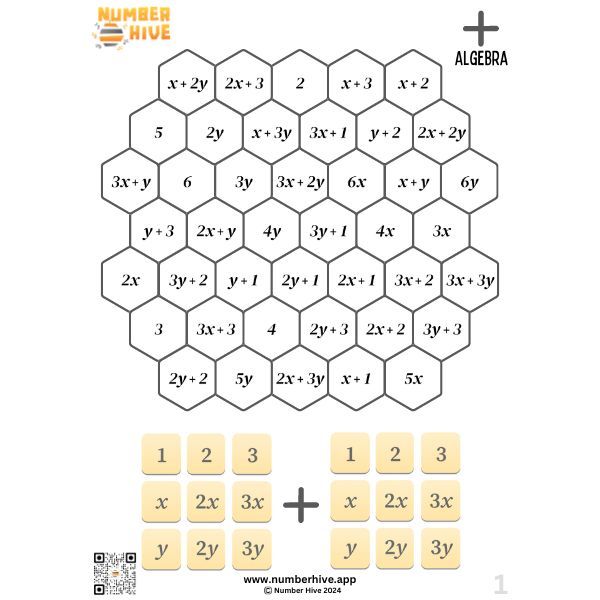
Addition: Algebra
Build fluency with algebraic operations (adding monomials). Foster a deep understanding of this foundational skill for any students studying higher levels of algebra down the track. Especially helpful for reinforcing that you can only add and subtract ‘like terms’.
Perfect for ages 11-14
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!

Addition: Linear Graphs
Slope and y-intercept y = mx + b
An engaging way for students to practice straight lines in slope-intercept form. Gets students thinking through what impact the coefficient and the constant term have on the graph.
Perfect for ages 12-16
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!

Gradient (Slope)
Help students gain a strong understanding of gradient in the form rise over run. A great pre-cursor to the Linear Graph activity.
Perfect for ages 12-16
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
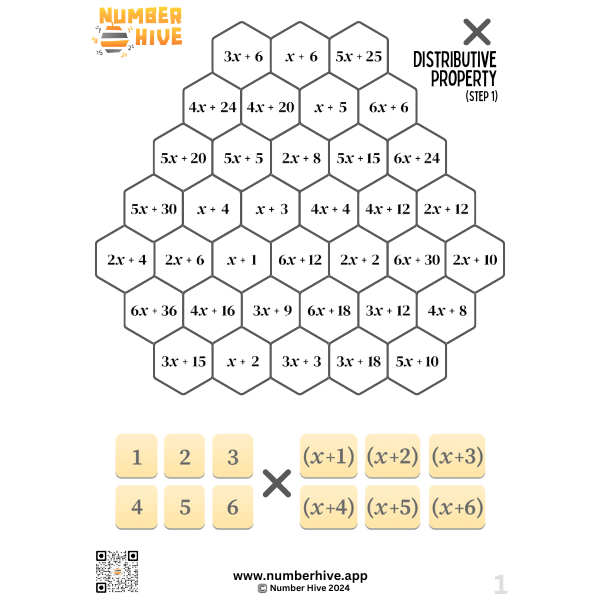
Multiplication of Algebra using the Distributive Property STEP 1
Build multiplicative fluency when using the Distributive Property with Algebra. Expanding brackets is such a foundational skill for any students studying higher levels of algebra down the track. Students also learn to find the highest common factor by working with the inverse operation.
This is step 1 of 5. Factor outside the brackets is positive and numerical. Inside the brackets, there’s only addition.
Perfect for ages 13-18
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
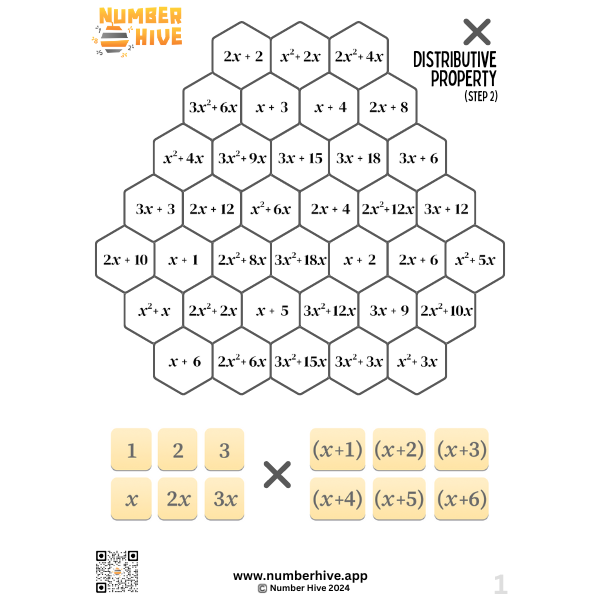
Multiplication of Algebra using the Distributive Property STEP 2
Build multiplicative fluency when using the Distributive Property with Algebra. Expanding brackets is such a foundational skill for any students studying higher levels of algebra down the track. Students also learn to find the highest common factor by working with the inverse operation.
This is STEP 2 of 5. Factor outside the brackets is positive. Inside the brackets, there’s only addition.
Perfect for ages 13-18
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
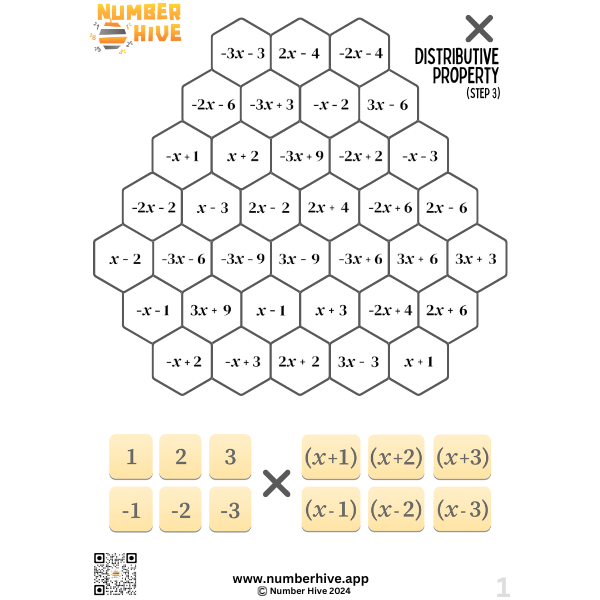
Multiplication of Algebra using the Distributive Property STEP 3
Build multiplicative fluency when using the Distributive Property with Algebra. Expanding brackets is such a foundational skill for any students studying higher levels of algebra down the track. Students also learn to find the highest common factor by working with the inverse operation.
This is STEP 3 of 5. Factors outside the brackets are positive and negative. Inside the brackets, there’s addition and subtraction.
Perfect for ages 13-18
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
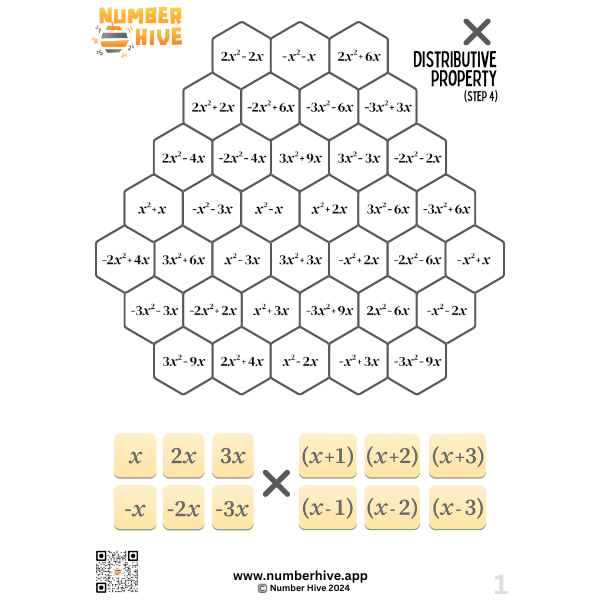
Multiplication of Algebra using the Distributive Property STEP 4
Build multiplicative fluency when using the Distributive Property with Algebra. Expanding brackets is such a foundational skill for any students studying higher levels of algebra down the track. Students also learn to find the highest common factor by working with the inverse operation.
This is STEP 4 of 5. Factors outside the brackets are positive and negative. Inside the brackets, there’s addition and subtraction.
Perfect for ages 14-18
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
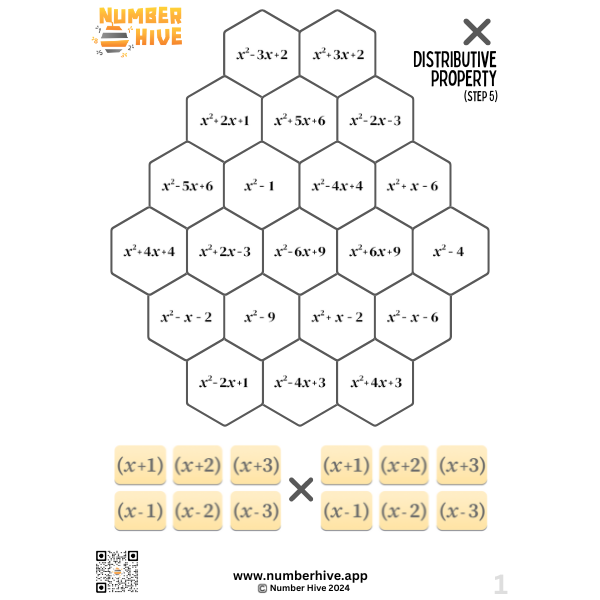
Multiplication of Algebra using the Distributive Property STEP 5
Build multiplicative fluency when using the Distributive Property with Algebra. Expanding brackets is such a foundational skill for any students studying higher levels of algebra down the track. In this version, students need to expand two sets of brackets.
This is STEP 5 of 5. Both factors are expressions involving addition and subtraction.
Perfect for ages 14-18
Choices include:
- Small Group Pack: 5 Game boards
- Class pack: 20 game boards (40 students)
Click here to watch a game!
Try Number Hive printable gameboards now! Download your free sample pack.
Have you played Number Hive online, yet?
Now available online, in the physical form, or better still – why not up your blended learning game to really drive differentiated learning in your class
Check out our blog for more student engagement tips, information about mathematics anxiety, and lots of other great content.
Join Our Community
Number Hive
How We Help
Resources
© Number Hive. All rights reserved.
Website made by Getmilk.